Rapide historique
La question de la calculabilité
Question fondamentale : "Qu'est-ce qui est calculable ?" (Wikipedia : Calculabilité)
Ou encore : "Peut-on automatiser la transformation d'informations grâce à une série des règles ?"
Selon Wikipedia (Thèse de Church), nous pouvons lire la définition suivante :
La thèse est formulée en disant que des règles formelles de calcul (machines de Turing, les fonctions λ-définissables, les fonctions récursives…) formalisent correctement la notion de méthode effective de calcul, ou de calculabilité.
On considère généralement[réf. nécessaire] que la notion intuitive de méthode effective de calcul correspond aux caractéristiques suivantes :
- l'algorithme consiste en un ensemble fini d'instructions simples et précises qui sont décrites avec un nombre limité de symboles ;
- l'algorithme doit toujours produire le résultat en un nombre fini d'étapes ;
- l'algorithme peut en principe être suivi par un humain avec seulement du papier et un crayon ;
- l'exécution de l'algorithme ne requiert pas d'intelligence de l'humain sauf celle qui est nécessaire pour comprendre et exécuter les instructions.
Plusieurs approches ont vu le jour :
- les fonctions récursives ;
- le lambda-calcul ;
- les machines de Turing ;
- les machines à compteurs ;
- les automates cellulaires ;
- les circuits booléens ;
- les machines parallèle à accès arbitraire ou PRAM ;
- les Random access machines ou RAM ;
- les machines de Blum-Shub-Smale.
De la question théorique à la création de machines à calculer
Deux approches ont durablement marqué la manière dont nous interagissons avec les ordinateurs :
- La machine d'Alan Turing qui pose les fondements des langages dits impératifs.
- Le lambda-calcul d'Alonzo Church qui pose les fondements des langages dits fonctionnels.
La machine de Turing
Un ruban infini, des case qui stockent des informations et une tête de lecture qui peut lire et écrire sur ces cases.
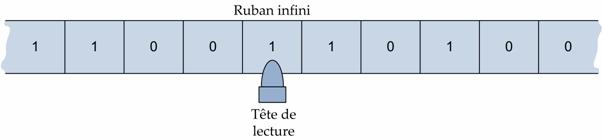
Un peu plus précisément, une machine de Turing se compose de :
- Un ruban infini.
- Une tête de lecture/écriture.
- Un registre d'état.
- Une table d'actions.
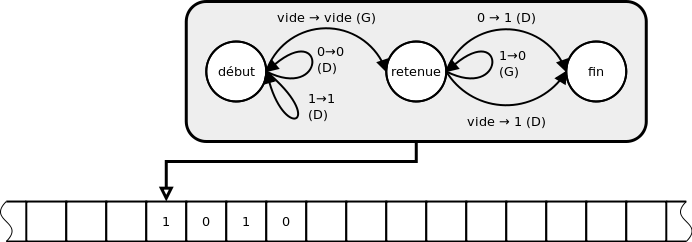
Et un petit exemple de machine de Turing en action.
L'ordinateur moderne est très similaire dans sa réalisation (Wikipedia : Les opération du processeur)

Langages fonctionnels (Church)
Le lambda-calcul est une approche plus abstraite de la calculabilité centré sur la fonction, au sens mathématique du terme.
Les idées fortes :
- On applique des fonctions à des termes.
- Une fonction peut elle-même être le terme d'une autre fonction.
- Les termes sont regroupés en expressions.
- Toute expression retourne une valeur ou une autre expression.


Les images sont tirées de cet article d'introduction au lambda-calcul (en anglais)